Qualitat de l’aire – Contaminació per NO₂ – Barcelona i Tarragona

L’objectiu principal és assolir un nivell de resolució alt, que permet simular les concentracions de contaminants a escala de carrer i permet:

• Avaluar l’evolució de lessituacions d’episodi ambiental i restriccions per contaminació.
• Avaluar la qualitat de l’aireamb més precisió a les zones urbanes principals.

Oferir informació bàsica als ciutadans i les ciutadanes de les emissions i immissions a les diferents zones de la seva ciutat.

Mitjançant models matemàtics, el model computacional utilitzarà les dades incorporades per a calcular la velocitat de vent i la concentració de NO₂ als carrers de la zona en estudi. El model requereix una sèrie de simplificacions, com ara obviar els fenòmens turbulents, però permet igualment obtenir una alta resolució de la qualitat de l’aire als carrers. Per aconseguir-ho consta de 3 etapes de càlcul:

Velocitat de vent (km/h)

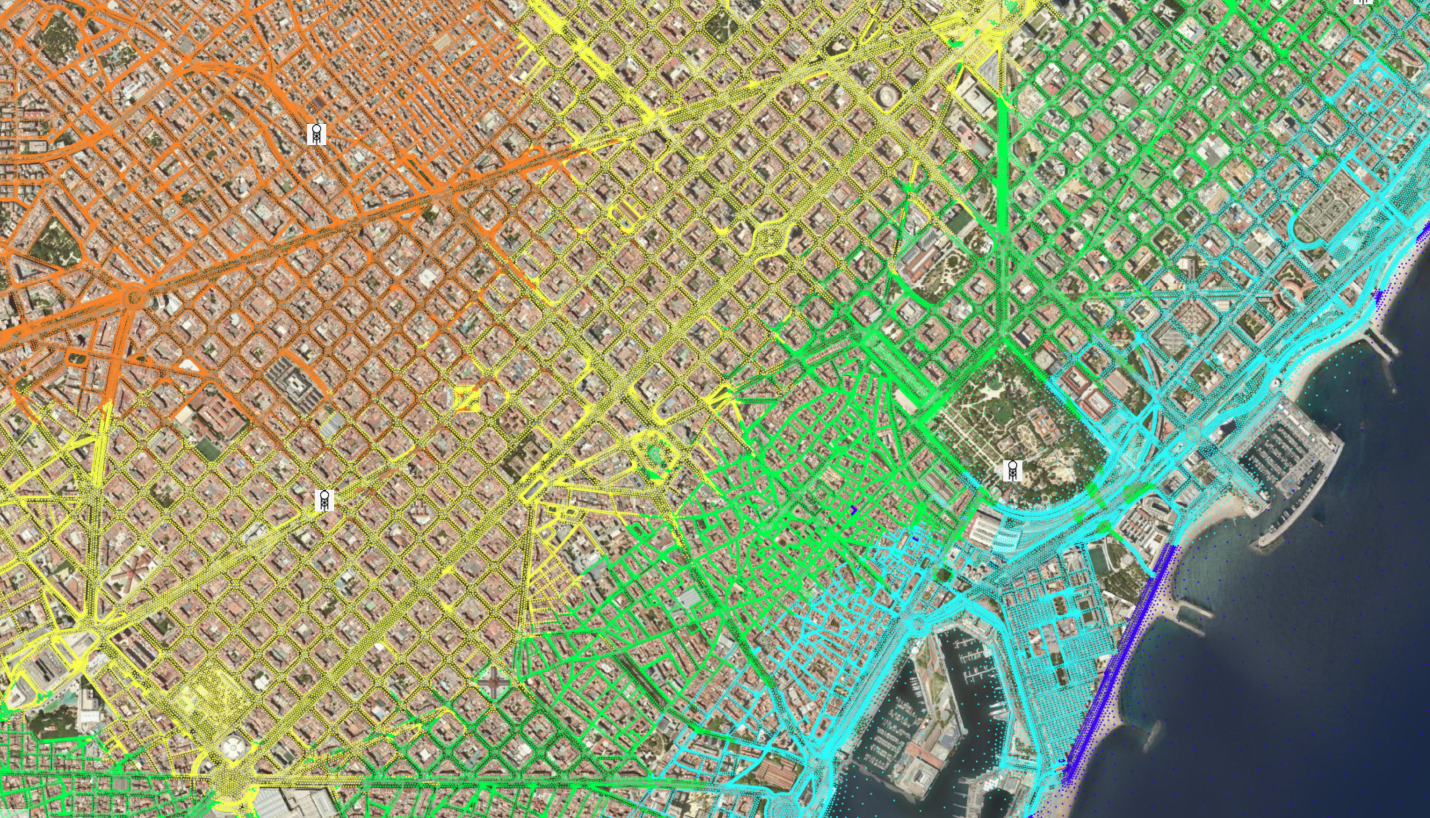
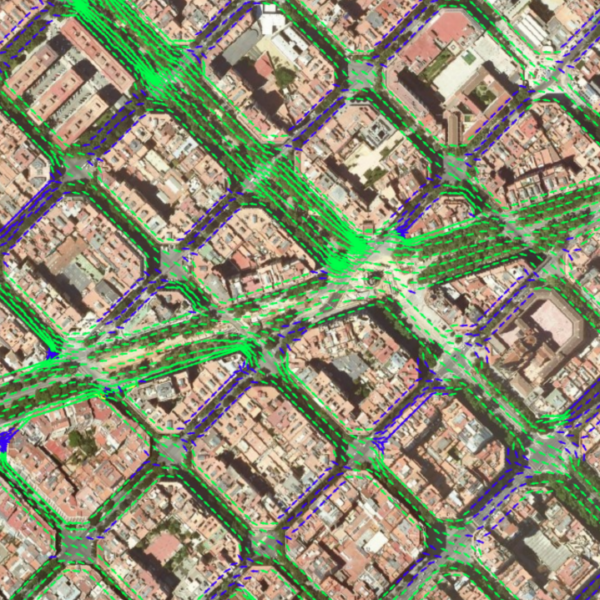
1. Velocitat del vent a 10 m d’alçada:Es parteix de les dades d’intensitat i direcció del vent recollides per Meteocat amb sensors a 10 m d’alçada (situats al terrat dels edificis) i es calcula la velocitat del venta tots els carrers de manera ràpida i robusta mitjançant l’equació de flux potencial. Aquesta equació permet simplificar la dinàmica de fluids i obviar la turbulència del vent.

Tot i que la turbulència del vent és important en el transport i la dinàmica dels contaminants, aquesta simplificació permet generar un model més fàcil sense privar el repte d’un pronòstic acurat i d’alta resolució per a la concentració de contaminants.

2. Estimació de la velocitat a 3,5 m d’alçada:Calcular la velocitat del vent a 10 m d’alçada permet obviar la fricció que el terra exerceix sobre el vent. La velocitat d’interès, però, es troba a 3,5 m d’alçada, i s’estima escalant la velocitat obtinguda a 10 m mitjançant la fórmula semi-empírica de Hellmann. 

Concentració de NO₂ (µg/m3)

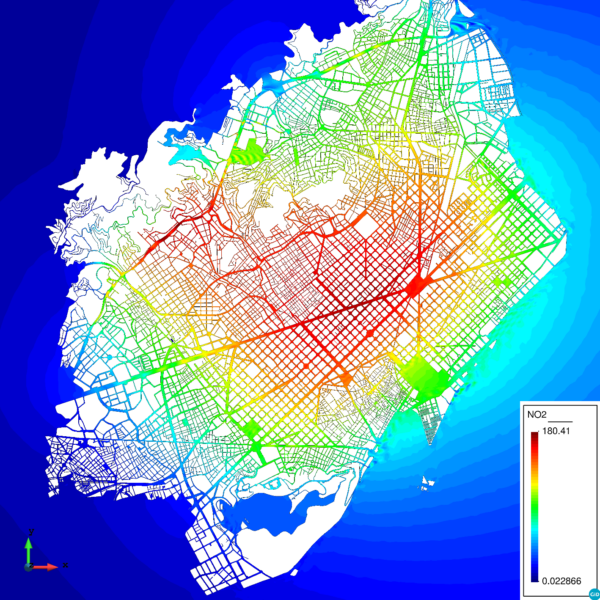
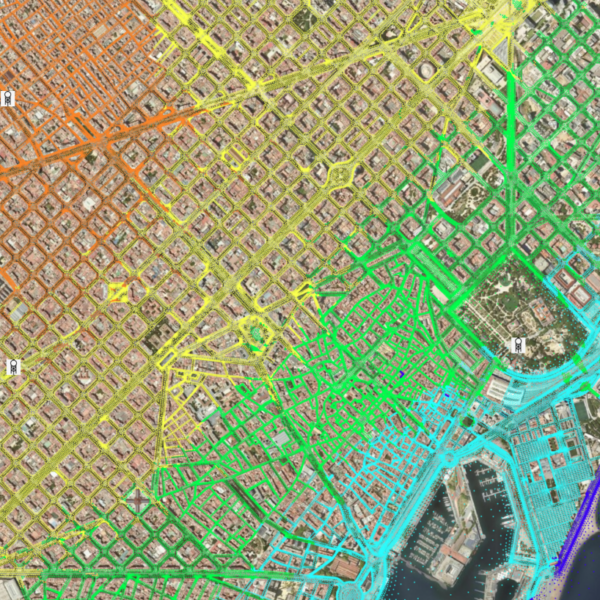
3. Transport de NO₂ als carrers de la zona d’estudi:Utilitzant les dades de trànsit i la velocitat del vent estimada a 3,5 m d’alçada, es calcula la concentració de NO₂en µg per m3 a cada punt dels carrers resolent l’equació de transport.

Aquesta equació permet incorporar fenòmens que afecten la dinàmica dels contaminants com ara el focus d’emissions (terme font) i possibles turbulències del vent que s’emporten part dels contaminants (terme d’absorció).

Mitjançant la resolució d’aquestes equacions, el model obté les concentracions i el transport de contaminants de NO2 teòrics i serà capaç de pronosticar l’evolució de la qualitat de l’aire amb una resolució alta. El model es valida mitjançant la comparació de les prediccions teòriques amb les dades reals de NO2 recollides a 3,5 m als carrers de les zones en estudi per la Xarxa de Vigilància i Previsió de la Contaminació Atmosfèrica (XVPCA), una xarxa d’estacions de mesura de contaminants de l’aire de la Generalitat.

Finalment, s’aconsegueix una eina amb una capacitat de predicció de 3 dies, que és capaç de realitzar una la simulació hora a hora i que servirà d’eina per a la gestió i la predicció del NO2, contaminant problemàtic a la ciutat de Barcelona i el Camp de Tarragona, tot i que es tracta d’un model escalable amb el qual es preveu ampliar la zona d’estudi.

Models computacionals

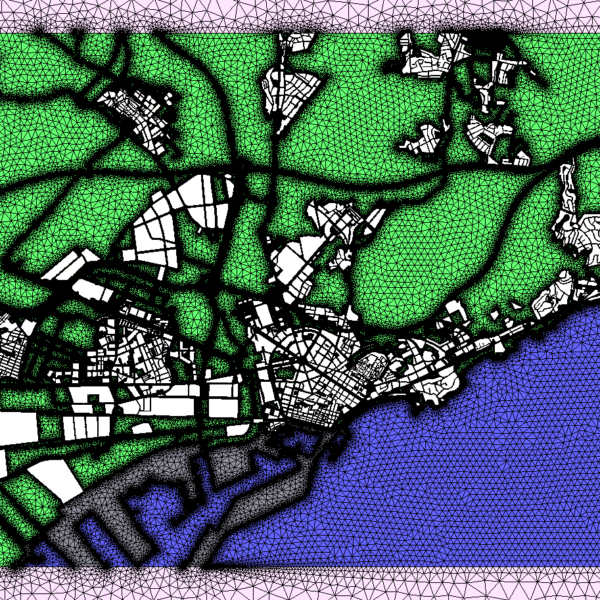
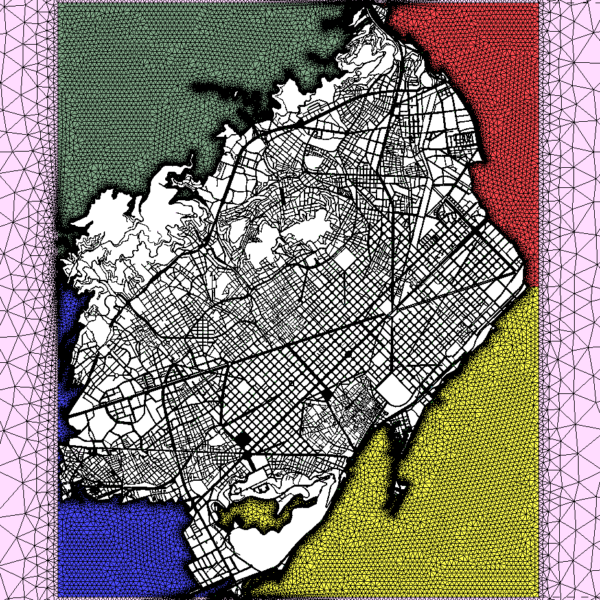
El model computacional segueix un mètode semi-Lagrangià basat en els elements finits. El mètode dels elements finits és un mètode de càlcul numèric que s’empra en la resolució d’equacions diferencials, basat en la discretització (o compartimentalització) del medi o de l’objecte en estudi en una malla d’elements connectats en nodes  (imatge superior) i que serveix per a resoldre problemes considerats continus.

D’aquesta manera, el model separa el territori en diferents seccions i forma una malla on les equacions matemàtiques seran resoltes per separat. Finalment, s’ensamblen els resultats per donar lloc a una solució per a un «problema» continu com és el vent que bufa als carrers de Barcelona o del Camp de Tarragona.

Mitjançant la resolució de les equacions amb el mètode d’elements finits, el model obté les concentracions i el transport de contaminants de NO2 teòrics i serà capaç de pronosticar l’evolució de la qualitat de l’aire amb una resolució alta. El model es valida mitjançant la comparació de les prediccions teòriques amb les dades reals de NO2 recollides a 3,5 m als carrers de les zones en estudi per la Xarxa de Vigilància i Previsió de la Contaminació Atmosfèrica (XVPCA), una xarxa d’estacions de mesura de contaminants de l’aire de la Generalitat.

Finalment, s’aconsegueix una eina amb una capacitat de predicció de 3 dies, que és capaç de realitzar una la simulació hora a hora i que servirà d’eina per a la gestió i la predicció del NO2, contaminant problemàtic a la ciutat de Barcelona i el Camp de Tarragona, tot i que es tracta d’un model escalable amb el qual es preveu ampliar la zona d’estudi.

Referències

Dadvand, P., Rossi, R., & Oñate, E. (2010). An object-oriented environment for developing finite element codes for multi-disciplinary applications. Archives of computational methods in engineering, 17(3), 253-297.

Idelsohn, S., Oñate, E., Nigro, N., Becker, P., & Gimenez, J. (2015). Lagrangian versus Eulerian integration errors. Computer Methods in Applied Mechanics and Engineering, 293, 191-206.

Puigferrat, A., de-Pouplana, I., & Oñate, E. (2020). FIC–FEM formulation for the multidimensional transient advection–diffusion–absorption equation. Computer Methods in Applied Mechanics and Engineering, 365, 112984.

Puigferrat, A., de-Pouplana, I., Amato, F., & Oñate, E. (2021). Numerical prediction of the distribution of black carbon in a street canyon using a semi-Lagrangian finite element formulation. Building and Environment, 199, 107910.

Zienkiewicz, O. C., Taylor, R. L., & Zhu, J. Z. (2005). The finite element method: its basis and fundamentals. Elsevier.

Contacte

Ignasi de Pouplana Sardà, Investigador postdoctoral a CIMNE, ipouplana@cimne.upc.edu

Salvador Latorre Sánchez, Investigador a CIMNE, latorre@cimne.upc.edu

Miguel Masó Sotomayor, Investigador doctoral a CIMNE mmaso@cimne.upc.edu

Eugenio Oñate Ibáñez de Navarra, Vicepresident de CIMNE, onate@cimne.upc.edu

Xavier Baulies Bochaca, Responsable de recerca i innovació VPDT, baulies@gencat.cat

Isabel Hernández Cardona, Subdirectora general de prevenció i control de la contaminació atmosfèrica isabel.hernandezc@gencat.cat

Xavier Guinart Primé, Cap del Servei de Vigilància i Control de l’Aire, xavier.guinart@gencat.cat

Eva M. Pérez Gabucio, Cap de la Secció d’Immissions, gabucio@gencat.cat

Cristina Alonso Rodríguez, Tècnica al Servei de Vigilància i Control de l’Aire, alonso@gencat.cat